Beier–Neely morphing algorithm
算法原理
主要算法流程如下:

因为有是生成中间帧,所以目标图是每一张中间帧,而原图为输入图像。为避免歧义,将输入图像称为 $src$ 和 $dst$。
简单地说,对于中间帧的每一个像素 $X$ ,对于每一条特征线,计算 $X$ 在 $src$ 和 $dst$ 基于该特征线的映射,然后加权平均算出最终在两图的映射 $X’$。然后使用 Bilinear 插值求出两个 $X’$ 的像素值,再加权平均求得 $X$ 最终的像素值。
生成中间帧特征线
这里根据帧数计算权重作 $src$ 和 $dst$ 特征线对的插值。设 $s$ 为特征线的起点,$e$ 为特征线的终点,则
$$ratio=i/n,i=1,\dots,n$$
$$s’=s_{src}\cdot(1-ratio)+s_{dst} \cdot ratio$$
$$e’=e_{src}\cdot(1-ratio)+e_{dst} \cdot ratio$$
计算 $X’$
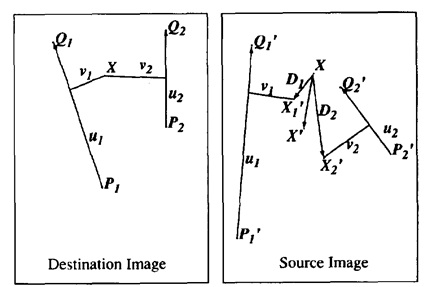
由上图可见,主要是通过 $X$ 在目标图中相对于特征线(向量)的位置,映射回原图对应特征线相对的位置。这个位置由 $X$ 在特征线上的投影和距离决定。
$$u=\frac{(X-P)\cdot(Q-P)}{||Q-P||^2}$$
$$v=\frac{(X-P)\cdot Perpendicular(Q-P)}{||Q-P||}$$
$$X’=P’+u\cdot(Q’-P’)+\frac{v\cdot Perpendicular(Q’-P’)}{||Q’-P’||}$$
$X’$ 的加权平均
通过下面的权重公式计算每一条特征线在当前 $X$ 中占的权重:
$$weight=( \frac{length^p}{a+dis})^b$$
其中 $a,b,p$ 为参数,我取的是 $1,2,0$,即权重与特征线的长度无关。
然后加到一个总的 $xsum$ 和 $weightsum$ 上
$$xsum =xsum+ X’ \cdot weight$$
$$weightsum=weightsum+weight$$
当所有特征线都遍历过后,就可以求出最终的 $X’$
$$X’=xsum/weightsum$$
Bilinear
这里是通过映射得到的 $X’$ 获得对应的 rgb。借用课件的图:
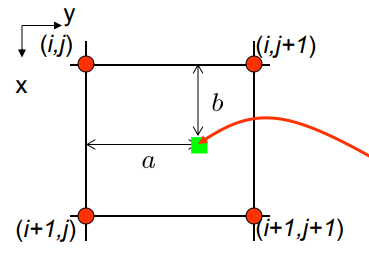
假设绿点为 $(x,y)$,对应的像素值为 $S(x,y)$,则有
$$S(x,y)=(1-a)\cdot(1-b)\cdot S(i,j)+a\cdot(1-b)\cdot S(i+1,j)+(1-a)\cdot b\cdot S(i,j+1)+a\cdot b\cdot S(i+1,j+1)$$
容易看出,这样插值当 $(x,y)$ 为任意一个顶点时,像素值即是该点的值。
像素值加权平均
在求得 $src$ 和 $dst$ 的像素值 $s_1,s_2$ 后,设当前帧数为 $i$,总帧数为 $n$ 。则 $X$ 的像素值为
$$s_x=s_1\cdot (1-\frac{i}{n})+s_2\cdot \frac{i}{n},i=1,\cdots, n$$
通过上面的算法步骤即可获得 Morphing 的中间帧。当然,在运行上面算法时还要自己标出特征线。
效果

评论